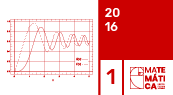
Ondas dispersivas – Korteweg – De – Vries (KDV)
Resumen
La presente investigación muestra el detalle de los cálculos obtenidos para una parte de la deducción de una de las ecuaciones más importantes de la actualidad en las Matemáticas, la ecuación de los científicos holandeses Diederick Johannes Korteweg y Gustav De Vries (KdV), llamada así en honor a estos destacados matemáticos. Esta deducción fué publicada en el año 1895 por la revista “Philosophical Magazine and Journal of Science” en Londres; la misma que con este trabajo venían a formalizar un hecho que se había puesto de manifiesto algunos años antes con un modelo matemático de ondas de agua sobre superficies poco profundas, conocidas como Solitones. Los Solitones tienen como principales características de que son ondas de gran amplitud cuya velocidad de propagación depende de su amplitud en contraposición a las ondas lineales, son dispersivas pero a su vez preservan su forma, son ondas de tipo onda solitaria, interactúan entre sí o con obstáculos finitos de tal manera que luego de la interacción recuperan totalmente sus propiedades previas a la interacción salvo cambios de fase. En la parte inicial de la investigación realizada, se presenta una introducción histórica sobre el origen de este fenómeno físico ocurrido en un canal de Escocia por Scott Russell; luego se deduce la variación del nivel del agua con respecto al tiempo, lo cual origina una ecuación diferencial parcial que permitirá encontrar la solución de la misma, para demostrar esta fórmula se empieza con la suposición de que las velocidades horizontal y vertical u y v del fluido pueden ser expresadas por series rápidamente convergentes. Finalmente, se determina la solución de la ecuación en la recta para ondas estacionarias, para esto se realiza el análisis de diferentes escenarios que podrían considerarse en la ecuación KdV, además para esta ecuación se emplean funciones elípticas que pueden ser vistas como una generalización de las funciones trigonométricas conocidas.
Citas
Boyd, J. P. "Solitons from Sine Waves: Analytical and Numerical Methods of Non-Integrable Solítary and Cnoidal Waves." Physica D 21, 227-246, 1986.
Gardner, C. S. "The Korteweg-de Vries Equation and Generalizations, IV. The Korteweg-de Vries Equation as a Hamiltonian System." J. Math. Phys. 12, 1548-1551, 1971.
Lax, P. "lntegrals of Nonlinear Evolution Equations and Solitary Waves." Comm. Pure Appl. Math. 21, 467-490 , 1968.
Miles, J. W. "The Korteweg-de Vries Equation, A Historical Essay." J. Fluid Mech. 106, 131-147, 1981.
Miura, R. M. "Korteweg-de Vries Equation and Generalizations. l. A Remarkable Explicit Nonlinear Transformation ." J. Math. Phys. 9, 1202-1204, 1968.
Russell, J. S. "Report on Waves." Report of the l4th Meeting of the British Association for the Advancement of Science. London: John Murray, pp. 311-390, 1844.